Examen final M2 MIAGE 20/05/2025¶
Durée : 3h. Calculatrices autorisées. Une feuille A4 manuscrite recto-verso autorisée.
Rappel : explicitez au moins un calcul de distance par exercice pour k-means et k-PPV.
1) Clustering¶
Soient les données
$$\begin{pmatrix}
x & y\\
9 & 5\\
2 & 2\\
6 & 8\\
8 & 4\\
6 & 5\\
7 & 8\\
7 & 3\\
\end{pmatrix}$$
Appliquez l'algorithme des k-means pour $K=2$ avec ces centres :
$$\begin{pmatrix}
x & y\\
3 & 5\\
6 & 8
\end{pmatrix}$$
Faites part de vos remarques et indiquez vos choix éventuels.
Comparez avec la partition obtenue via l'algorithme CAH en utilisant single linkage d'abord, puis complete linkage. Décrivez les étapes et tracez les dendrogrammes.
2) Chaînes de Markov¶
Alice et Bob participent à une course automobile. Le parcours comporte une alternance de lignes droites notées $L$ et virages notés $V$. On considère dans cet exercice la configuration $LVLV$. Dans chaque virage un.e pilote choisit de rouler à une vitesse (normalisée) $v \in ]0,1]$, et risque d'avoir un accident l'empêchant de continuer avec probabilité $v^2$. En ligne droite on suppose que tous les deux roulent à leur vitesse maximum commune. On considère la largeur de la route négligeable (on n'en tient pas compte).
La progression d'un.e pilote est-elle modélisable par une chaîne de Markov ? Justifiez. Explicitez la chaîne le cas échéant (états et transitions).
Alice roule en choissant toujours $v_A = 0.5$ en virage. Quelle est sa probabilité $P_A$ de terminer la course indemne (indiquez le calcul en l'expliquant) ? Donnez l'allure du graphe de $P_A$ en fonction de $v_A \in ]0,1]$. On suppose désormais et jusqu'à la fin de l'exercice que $v_A$ est quelconque dans $]0,1]$ mais fixé.
Les données du problème permettent-elles de calculer un temps de parcours connaissant les vitesses ? Si non, indiquez ce qui manque.
Connaissant la vitesse d'Alice $v_A$, Bob dispose-t-il d'une stratégie lui permettant de gagner à coup sûr ? Si oui : laquelle ? Et si non, pourquoi ?
Toujours connaissant $v_A$, Bob aimerait terminer la course devant Alice avec une probabilité $ > 0.5$. Comment peut-il procéder ? Justifiez.
3) k plus proches voisins : classification¶
Soient les données $$\begin{pmatrix} x & y & \mbox{classe}\\ 5 & 7 & 2\\ 6 & 6 & 1\\ 7 & 4 & 2\\ 4 & 2 & 1\\ 0 & 8 & 2\\ 9 & 5 & 2\\ 2 & 0 & 1\\ 1 & 3 & 2\\ 3 & 9 & 1\\ 8 & 1 & 2 \end{pmatrix}$$ Prenant $k=3$, considérez d'abord les 4 premières rangées comme l'ensemble de test, puis les 4 dernières. Dans les deux cas calculez le taux d'erreur.
Pourquoi est-il plus judicieux de choisir $k$ impair dans le cas d'une classification binaire ?
4) Arbre de décision : classification¶
Soient les données $$\begin{pmatrix} x & y & z\mbox{ (cible)}\\ 3 & B & 1\\ 1 & A & 1\\ 5 & C & 3\\ 2 & B & 1\\ 5 & B & 3\\ 1 & B & 2\\ 5 & B & 2\\ 3 & C & 1\\ 4 & A & 3 \end{pmatrix}$$ Les colonnes x et y sont respectivement numérique et symbolique. Il y a trois classes en sortie : colonne 'z'.
Construisez l'arbre de décision associé (avec le critère Gini rappelé ci-dessous), et dessinez-le.
$\mbox{Gini}(p_1, \dots, p_k) = 1 - \sum_{j=1}^{k} p_j^2$
Corrigé
Clustering¶
Barême 0.5 calculs distances + 1.5 k-means + 2 x 1.5 CAH
import matplotlib.pyplot as plt
# Données : x, y, classe
points = [
(9, 5),
(2, 2),
(6, 8),
(8, 4),
(6, 5),
(7, 8),
(7, 3)
]
centers = [
(3, 5),
(6, 8),
(5, 10/3),
(7.5, 6.25),
(4.5, 2.5),
(7.2, 6)
]
# Lettres de A à J
labels_pts = [chr(65 + i) for i in range(len(points))]
labels_ctrs = ['c1_1', 'c2_1', 'c1_2', 'c2_2', "c1_2'", "c2_2'"]
# Séparer les coordonnées et les classes
x_vals_pts = [p[0] for p in points]
y_vals_pts = [p[1] for p in points]
x_vals_ctrs = [p[0] for p in centers]
y_vals_ctrs = [p[1] for p in centers]
# Tracer les points + centres
plt.figure(figsize=(8, 6))
for i in range(len(points)):
plt.scatter(x_vals_pts[i], y_vals_pts[i], color='blue', s=100)
plt.text(x_vals_pts[i] + 0.2, y_vals_pts[i], labels_pts[i], fontsize=12, verticalalignment='center')
for i in range(4):
plt.scatter(x_vals_ctrs[i], y_vals_ctrs[i], color='red', s=100)
plt.text(x_vals_ctrs[i], y_vals_ctrs[i] - 0.4, labels_ctrs[i], fontsize=12, verticalalignment='center')
for i in range(2):
plt.scatter(x_vals_ctrs[i+4], y_vals_ctrs[i+4], color='green', s=100)
plt.text(x_vals_ctrs[i+4], y_vals_ctrs[i+4] - 0.4, labels_ctrs[i+4], fontsize=12, verticalalignment='center')
# Axes
plt.xlabel('x')
plt.ylabel('y')
plt.title('Affichage des points et des centres')
plt.grid(True)
plt.axis('equal')
plt.show()
k-means¶
$F$ et $A$ sont graphiquement plus proches du centre 2 que du 1. De même, $B$ est plus proche de A que de $c_2$. Calculons les 2 x trois autres distances :
$d^2(E,c_1) = d^2(E,c_2) = 9$, donc il faut affecter le point $E$ arbitrairement. Choisissons le cluster 1.
$d^2(D, c_1) = 26$ et $d^2(D, c_2) = 20$ donc $D$ rejoint $C_2$.
$d^2(G, c_1) = 20$ et $d^2(G,c_2) = 26$ donc $G$ rejoint $C_1$.
Premier découpage : $C_1 = (B, E, G)$ et $C_2 = (C, F, A, D)$.
Recalul des centres : $c_1 \leftarrow ( (2+6+7)/3, (2+5+3)/3 ) \simeq (5, 3.33)$, $c_2 \leftarrow ( (6+7+9+8)/4, (8+8+5+4)/4 ) = (7.5, 6.25)$. La seule ambiguité graphique concerne à nouveau le point $E$ : $d^2(E, c_1) = 1 + (5/3)^2 = 34/9 \simeq 3.78 $ et $d(E, c_2) = 1.5^2 + 1.25^2 \simeq 3.81$ donc $E$ reste dans $C_1$, et l'algorithme a convergé.
Remarque : tant qu'on y est, regardons ce qui se serait passé si on avait affecté $E$ à $C_2$. Alors la mise à jour des centres donne $c_1 \leftarrow ( (2+7)/2, (2+3)/2 ) = (4.5, 2.5)$, $c_2 \leftarrow ( (6+6+7+9+8)/5, (5+8+8+5+4)/5 ) = (7.2, 6)$. C'est en fait un peu plus facile puisqu'on ne détecte pas d'ambiguité graphique (à la limite pour $G$, mais on voit qu'il est alors plus proche de $c_1$). C'est intéressant, on converge encore en une itération mais vers des groupes différents.
CAH¶
$C$ et $F$ fusionnent en premier pour les deux versions de l'algorithme car ce sont les points les plus proches (distance 1). Ensuite $d(D,A) = d(D,G)$ et c'est clairement la plus petite seconde distance ($\sqrt{2}$). Il faut donc faire un choix : disons $A$ avec $D$. C'est à partir de là que single linkage (SL) et complete linkage (CL) diffèrent.
SL : $G$ rejoint le cluster $A, D$ (coût $\sqrt{2}$), puis $E$ (coût $\sqrt{5}$), puis $C,F$ (coût $\sqrt{9} = 3$), et enfin $B$ se rallie au groupe (coût $\sqrt{25} = 5$). Remarquons qu'en faisant l'autre choix ($D$ avec $G$), le résultat est le même en inversant $A$ et $G$.
CL : Graphiquement $d(E, G) < d(E, A)$ et $d(E,G) < d(G,A)$ donc la fusion suivante concerne $E$ et $G$ (coût $\sqrt{5}$). Ensuite, la "plus courte longue distance" est soit $d(A,E)$ soit $d(A,G)$ : dans les deux cas $(A,D)$ et $(E,G)$ fusionnent (coût $\sqrt{9} = 3$ avec $A-E$). Si on avait choisi $D,G$ au lieu de $D,A$ alors l'ordre aurait été $E \rightarrow D,G$ (coût $\sqrt{5}$) puis $A \rightarrow E,D,G$ (coût $\sqrt{9} = 3$). Finalement on doit comparer $d^2(C,G) = 26$ et $d^2(B,A) > 49$ : cela achève l'algorithme. Le coût de la dernière fusion est égale à la distance $d(B,F) = \sqrt{61}$ ($d(B,A) = \sqrt{58}$).
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
from scipy.spatial.distance import pdist
# Données (identiques à la matrice R)
d = np.array([
[9, 5],
[2, 2],
[6, 8],
[8, 4],
[6, 5],
[7, 8],
[7, 3]
])
# Labels alphabétiques
labels = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
# Calcul des distances
distances = pdist(d)
# CAH avec méthode "single"
h1 = linkage(distances, method='single')
# CAH avec méthode "complete"
h2 = linkage(distances, method='complete')
# Affichage des deux dendrogrammes
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
dendrogram(h1, labels=labels)
plt.title("Single linkage")
plt.subplot(1, 2, 2)
dendrogram(h2, labels=labels)
plt.title("Complete linkage")
plt.tight_layout()
plt.show()
Les deux versions de l'algorithme CAH donnent la même partition pour $k = 2$ et $k = 3$. Ils ne diffèrent qu'à partir de $k = 4$, où $E$ est isolé dans le cas single linkage.
Cette partition pour $k = 2$ est très différente de celle obtenue par k-means : beaucoup plus déséquilibrée.
Markov¶
Barême 1.5 + 1 + 0.5 + 0.5 + 1.5.
1] Conditionnellement au fait qu'un.e pilote soit toujours sur la piste, son avenir ne dépend que de l'état courant : rien dans l'énoncé ne laisse suggérer le contraire (par exemple, qu'il ait peur de rouler à plus de 90 km/h s'il a déjà dépassé 100 km/h, etc). Une chaîne de Markov telle qu'étudiée en cours semble donc appropriée. Ensuite on voit que seuls les virages ont un intérêt, car en ligne droite la vitesse commune est imposée et l'énoncé n'indique pas de possibilité d'accident (on déduit qu'il n'y en a pas). Le parcours donné se réduit donc à $VV$ du point de vue de l'étude mathématique. On ajoute un état "I" comme "initial", avec une transition de probabilité 1 vers le premier virage $V_1$. Ensuite depuis $V_1$ on peut avoir un accident ou bien atteindre le second virage, depuis lequel une fois encore on arrive à $A$ ou bien $F$ : état final, course terminée.
Vous pouviez aussi garder des états $L_1$ et $L_2$ pour les lignes droites (inutile mais pourquoi pas), ou démarrer en $V_1$ sans introduire d'état initial : tout cela est correct également. Il fallait bien indiquer les probabilités de transition en revanche : $1 - v_1^2$ etc.
import networkx as nx
import matplotlib.pyplot as plt
# Note : amélioration des self loops possible :
# https://stackoverflow.com/questions/74350464/how-to-better-visualize-networkx-self-loop-plot
# Création du graphe orienté
G = nx.DiGraph()
# Ajout des états
states = ['I', 'V1', 'V2', 'A', 'F']
G.add_nodes_from(states)
# Ajout des transitions avec leurs probabilités
G.add_edge('I', 'V1', weight='1')
G.add_edge('V1', 'V2', weight='1 - v1^2')
G.add_edge('V1', 'A', weight='v1^2')
G.add_edge('V2', 'F', weight='1 - v2^2')
G.add_edge('V2', 'A', weight='v2^2')
G.add_edge('A', 'A', weight='1')
G.add_edge('F', 'F', weight='1')
# Positions des nœuds pour une visualisation claire
pos = {
'I': (0, 0),
'V1': (1, 0),
'V2': (2, 0),
'F': (3, 1),
'A': (3, -1)
}
# Tracer le graphe
plt.figure(figsize=(10, 6))
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=2000, font_size=12, arrowsize=20)
# Ajouter les étiquettes de poids (probabilités)
edge_labels = {(u, v): d["weight"] for u, v, d in G.edges(data=True)}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=12)
plt.title("Chaîne de Markov : Course automobile")
plt.axis('off')
plt.show()
2] $P_A$ = probabilité de ne pas avoir d'accident, ni dans le premier virage ni dans le second, ce qui nous mène à l'état $F$. D'après l'énoncé (ou le graphe juste tracé) cette probabilité s'écrit $(1 - v_A^2)^2$. On pourrait aussi utiliser la méthode générale vue en cours avec les matrices $N$, $R$ et $Q$ mais c'est un peu overkill ici. Ensuite on remplace $v_A$ par $0.5$ : $P_A = \left( \frac{3}{4} \right)^2 = \frac{9}{16}$.
import numpy as np
import matplotlib.pyplot as plt
# Note : la question demande l'allure (générale), si vous n'avez pas le changement de convexité final
# vers 0.8 c'est ok aussi. Il fallait voir la décroissance et reporter le point (1/2, 9/16) au minimum.
# (avec f(0) = 1 et f(1) = 0).
# Définir la fonction
def f(x):
return (1 - x**2)**2
# Générer des valeurs x dans l'intervalle ]0,1]
x = np.linspace(0.001, 1, 500) # Évite x=0 pour éviter division par zéro
# Calcul des valeurs f(x)
y = f(x)
# Tracer la courbe
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=r'$f(x) = (1 - x^2)^2$', color='darkblue')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Courbe de f(x) = (1 - x²)² sur ]0,1]')
plt.grid(True)
plt.legend()
plt.show()
3] Non : Il manque les longueurs des virages (et des lignes droites !). Le temps de course s'écrit comme la somme de ces longueurs divisées par les vitesses correspondantes (dans une unité à définir), mais l'énoncé ne demandait pas le calcul.
4] Non : quelle que soit la vitesse choisie par Bob dans les virages, il peut avoir un accident avec une probabilité non nulle ($v^2 > 0$ car $v \in ]0,1]$ par hypothèse dans l'énoncé). N'étant jamais complètement sûr de terminer la course $-$ d'après la modélisation imposée ! $-$ il n'est jamais 100% sûr de gagner.
5] Déterminons d'abord la valeur $v_A$ donnant $P_A = 0.5$ : il faut résoudre l'équation $(1-v_A^2)^2 = 0.5$, soit $1 - v_A^2 = \sqrt{0.5}$ puis $v_A = \sqrt{1 - \sqrt{0.5}} \simeq 0.54$. Notons cette valeur (exacte) $v_0$. Il s'agit de la vitessse à laquelle Alice termine la course sans accident avec probabilité 0.5. On peut aussi effectuer une lecture graphique et dire que $v_0$ vaut environ 0.55 $-$ j'accepterai cette méthode aussi car la valeur exacte n'a pas grand intérêt ici. On note $P^{(G)}$ la probabilité que Bob l'emporte.
Premier cas : Alice roule à une vitesse $> v_0$.
Alors Bob peut décider de rouler très lentement afin d'être presque sûr de finir la course : cela suffit à gagner avec probabilité $> 0.5$. Montrons le mathématiquement (je compterai juste si vous aviez l'intuition). Soit $v_B \in ]0,1]$ la vitesse de Bob dans chaque virage. Alors, par hypothèse d'indépendance la probabilité qu'il termine la course et qu'Alice ait un accident s'écrit comme le produit $P_B (1 - P_A)$, soit $P^{(G)} = (1 - v_B^2)^2 (1 - P_A)$. $P_A < 0.5$ donc $1 - P_A > 0.5$ : écrivons $1 - P_A = 0.5 + \delta$ avec $\delta > 0$, puis
$$ \begin{align*}
P^{(G)} &= (1 - v_B^2)^2 \, (0.5 + \delta)\\
&= (1 + v_B^4 - 2 v_B^2) \, (0.5 + \delta)\\
&= 0.5 + \delta + v_B^4 \, (0.5 + \delta) - 2 v_B^2 \, (0.5 + \delta)\\
&> 0.5 + \delta - 2 v_B^2 \, (0.5 + \delta)
\end{align*}$$
Choisissons $v_B = \sqrt{ \frac{\delta}{2 + 4 \delta} } \in ]0,1]$ de manière à ce que $2 v_B^2 = 0.5 \frac{\delta}{0.5 + \delta}$ : alors
$$P^{(G)} > 0.5 + \delta - 0.5 \frac{\delta}{0.5 + \delta} \, (0.5 + \delta) = 0.5 + 0.5 \delta > 0.5 \, .$$
Second cas : Alice roule exactement à vitesse $v_0$.
Alors si Bob roule moins vite, il est sûr d'être battu par Alice avec probabilité 0.5 (il suffit qu'elle termine la course). S'il roule plus vite il aura un accident avec probabilité $> 0.5$, et enfin s'il roule lui aussi à $v_0$ sa probabilité de victoire s'écrit $P^{(G)} = 0.5 \times 0.5 < 0.5$. Impossible d'assurer la "victoire statistique" dans ces conditions.
Troisième cas : Alice roule (strictement) moins vite que $v_0$.
Choisissons alors $v_B = \frac{v_A + v_0}{2}$ : $v_B < v_0$ donc Bob termine la course avec probabilité $P_B > 0.5$. Mais s'il termine alors il est sûr de gagner car il a roulé plus vite qu'Alice.
Finalement, Bob dispose d'une stratégie "statistiquement gagnante" du moment que $v_A \neq v_0$.
k-PPV¶
Barême : 0.5 pour k=3, 0.5 par voisinage + classe prédite juste, 0.5 pour au moins un calcul de distance OK.
import matplotlib.pyplot as plt
# Données : x, y, classe
points = [
(5, 7, 2),
(6, 6, 1),
(7, 4, 2),
(4, 2, 1),
(0, 8, 2),
(9, 5, 2),
(2, 0, 1),
(1, 3, 2),
(3, 9, 1),
(8, 1, 2)
]
# Lettres de A à J
labels = [chr(65 + i) for i in range(len(points))]
# Séparer les coordonnées et les classes
x_vals = [p[0] for p in points]
y_vals = [p[1] for p in points]
classes = [p[2] for p in points]
# Couleurs selon la classe
colors = ['blue' if c == 1 else 'red' for c in classes]
# Tracer les points
plt.figure(figsize=(8, 6))
for i in range(len(points)):
plt.scatter(x_vals[i], y_vals[i], color=colors[i], s=100)
plt.text(x_vals[i] + 0.2, y_vals[i], labels[i], fontsize=12, verticalalignment='center')
# Légende personnalisée
from matplotlib.lines import Line2D
legend_elements = [
Line2D([0], [0], marker='o', color='w', label='Classe 1', markerfacecolor='blue', markersize=10),
Line2D([0], [0], marker='o', color='w', label='Classe 2', markerfacecolor='red', markersize=10)
]
plt.legend(handles=legend_elements)
# Axes
plt.xlabel('x')
plt.ylabel('y')
plt.title('Affichage des points avec étiquettes et classes')
plt.grid(True)
plt.axis('equal')
plt.show()
1] Test = $A, B, C, D$ :
$A$ a pour PPV $I$, $E$ et $F$ (analyse visuelle) de classes 1, 2, 2 donc le vote majoritaire sélectionne la classe 2 : pas d'erreur.
$B$ a pour PPV $F$ et $I$ (lecture graphique). Ensuite, le seul point bleu restant est plus loin que $H$ par exemple : on fera donc une erreur.
$C$ : $F$ et $J$ sont les plus proches, de classe 2 => pas d'erreur.
$D$ : PPV = $H$, $G$, $J$ de classe majoritaire 2 => erreur.
Taux d'erreur = 2/4 = 50%.
2] Test = $G, H, I, J$ :
$G$ a pour PPV $D$ puis $C$. Ensuite il faut calculer $d(G, B)$ et $d(G, A)$ pour être sûr : $d^2(G, B) = 4^2 + 6^2 = 50$ et $d^2(G, A) = 3^2 + 7^2 = 58$ => $B$ est le 3eme plus proche, donc on prédit 1 : pas d'erreur.
$H$ : PPV = $D$. Ensuite si $d(H, B)$ se classe parmi les 2 plus courtes distances aux voisins suivantes alors on prédit 1, sinon 2. Calculons :
$d^2(H, B) = 5^2 + 3^2 = 34$, $d^2(H, A) = 2 \times 4^2 = 32$, $d^2(H, C) > 6^2 = 36$, $d^2(H, E) = 5^2 + 1 = 26$.
Conclusion : on prédit 2 => pas d'erreur.
$I$ a pour PPV $A$ et $E$ de l'autre classe, donc on fera une erreur.
$J$ a pour PPV $C$, $F$ et $D$ de classe majoritaire 2 => pas d'erreur.
Le taux d'erreur change : 25% cette fois (d'où l'intérêt de la validation croisée).
=====
Il vaut mieux choisir $k$ impair pour éviter les ex-aequos : ainsi il y a toujours une classe majoritaire.
Arbres¶
Barême : 1 point par découpe juste (avec calculs OK) + 0.5 pour le dessin (juste !) + 0.5 remarque feuille impure impasse.
Commençons par l'attribut $y$ : il faut essayer les trois découpages, $A$ vs $B, C$ etc.
$$\begin{pmatrix} y & z\mbox{ (cible)}\\ A & 1\\ A & 3\\ B & 1\\ B & 1\\ B & 3\\ B & 2\\ B & 2\\ C & 3\\ C & 1 \end{pmatrix}$$
$\Delta_{A,B-C} = (2/9) (2 \times (1/2)^2) + (7/9) ((3/7)^2 + 2 \times (2/7)^2) = 7/(9 \times 7) + 17/(9 \times 7) = 24/63 = 8/21 \simeq 0.38$
$\Delta_{B,A-C} = (5/9) (2 \times (2/5)^2 + (1/5)^2) + (4/9) (2 \times (1/2)^2) = 9/45 + 10/45 = 19/45 \simeq 0.42$
$\Delta_{C,A-B} = \Delta_{A,B-C}$ car les cibles sont les mêmes pour $y = A$ et $y = C$.
Découpons ensuite selon $x$ : on commence par trier.
$$\begin{pmatrix} x & z\mbox{ (cible)}\\ 1 & 1\\ 1 & 2\\ 2 & 1\\ 3 & 1\\ 3 & 1\\ 4 & 3\\ 5 & 3\\ 5 & 3\\ 5 & 2 \end{pmatrix}$$
On observe plusieurs répétitions : c'est plutôt une bonne nouvelle du point de vue alorithmique car ça limite les coupes possibles. (Mais c'est aussi le signe d'une colonne peu discriminante). On essaye entre 1 et 2 puis entre 3 et 4 ; nous savons que la découpe entre 2 et 3 sera moins intéressante que les autres (cf. supplément posté sur Discord), de même que celle entre 4 et 5 : coupe entre deux valeurs identiques de la cible.
$\Delta_{1,2} = (2/9) (2 \times (1/2) ) + (7/9) (2 \times (3/7)^2 + (1/7)^2) = 7/63 + 19/63 = 26/63 \simeq 0.41$
$\Delta_{3,4} = (5/9) ( (4/5)^2 + (1/5)^2 ) + (4/9) ( (3/4)^2 + (1/4)^2 ) = 68/180 + 50/180 = 118 / 180 \simeq 0.66$
Conclusion : la première coupe se fait selon $x < 3.5$.
=====
Groupe "gauche" $x < 3.5$ :
$$\begin{pmatrix} y & z\mbox{ (cible)}\\ A & 1\\ B & 1\\ B & 1\\ B & 2\\ C & 1 \end{pmatrix}$$
On voit que "$B$ vs. le reste" est la découpe la plus intéressante, puisqu'elle mène à la répartition $1,1 - 1,1,2$ au lieu de $1 - 1,1,1,2$. Calculons le gain d'information (à constante près) :
$\Delta_{B,A-C} = (2/5) + (3/5) ((2/3)^2 + (1/3)^2) = 6/15 + 5/15 = 11/15 \simeq 0.73$
Ensuite selon $x$ :
$$\begin{pmatrix} x & z\mbox{ (cible)}\\ 1 & 1\\ 1 & 2\\ 2 & 1\\ 3 & 1\\ 3 & 1 \end{pmatrix}$$
Comme vu précédemment la coupe entre 2 et 3 n'a pas d'intérêt. On calcule donc le gain pour l'autre :
$\Delta_{1,2} = (2/5) (2 \times (1/2)^2) + 3/5 = 4/5 = 0.8$.
On continue donc à gauche suivant $x < 1.5$. Terminons cette branche : le noeud $x > 1.5$ est pur, et de l'autre côté les deux lignes $(x, z)$ restantes sont identiques donc c'est une impasse. Par chance on peut terminer selon $y$ :
$$\begin{pmatrix} y & z\mbox{ (cible)}\\ A & 1\\ B & 2 \end{pmatrix}$$
Règle finale : $y = A$ vs. $y \neq A$ (choix arbitraire).
=====
À droite ensuite :
$$\begin{pmatrix} y & z\mbox{ (cible)}\\ A & 3\\ B & 3\\ B & 2\\ C & 3 \end{pmatrix}$$
$B$ vs. le reste est meilleur que les deux autres découpes, car dans un cas on a $3,3 - 2,3$ et dans l'autre $3 - 2,3,3$. Calculons le gain d'information :
$\Delta_{B,A-C} = (1/2) (2 \times (1/2)^2) + 1/2 = 3/4 = 0.75$.
Puis selon $x$ :
$$\begin{pmatrix} y & z\mbox{ (cible)}\\ 4 & 3\\ 5 & 3\\ 5 & 3\\ 5 & 2 \end{pmatrix}$$
La seule découpe possible mène à $3 - 3,3,2$ : on en déduit qu'il faut préférer $y$. Le noeud correspondant à $y \neq B$ est pur (classe 3) ; on se concentre donc sur les données restantes :
$$\begin{pmatrix} x & y & z\mbox{ (cible)}\\ 5 & B & 3\\ 5 & B & 2 \end{pmatrix}$$
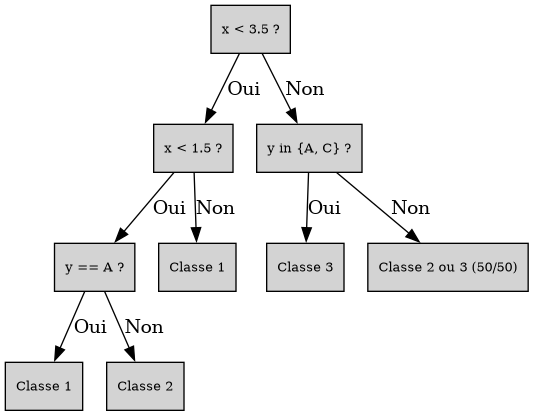
Les deux lignes sont identiques (sauf la valeur cible) : il y a une incohérence dans les données, on ne peut pas aller plus loin. On indiquera "50% 3, 50% 2" dans cette feuille.
from graphviz import Digraph
# Création du graphe
dot = Digraph()
dot.attr('node', shape='box', style='filled', fillcolor='lightgrey', fontsize='10')
# Noeuds
dot.node('N1', 'x < 3.5 ?')
dot.node('N2', 'x < 1.5 ?')
dot.node('N3', 'y == A ?')
dot.node('L1', 'Classe 1') # y == A
dot.node('L2', 'Classe 2') # y != A
dot.node('L3', 'Classe 1') # x ≥ 1.5
dot.node('N4', 'y in {A, C} ?')
dot.node('L4', 'Classe 3')
dot.node('L5', 'Classe 2 ou 3 (50/50)')
# Arcs
dot.edge('N1', 'N2', label='Oui')
dot.edge('N2', 'N3', label='Oui')
dot.edge('N3', 'L1', label='Oui')
dot.edge('N3', 'L2', label='Non')
dot.edge('N2', 'L3', label='Non')
dot.edge('N1', 'N4', label='Non')
dot.edge('N4', 'L4', label='Oui')
dot.edge('N4', 'L5', label='Non')
# Affichage
dot.render('arbre_decision', format='png', view=False)
'arbre_decision.png'