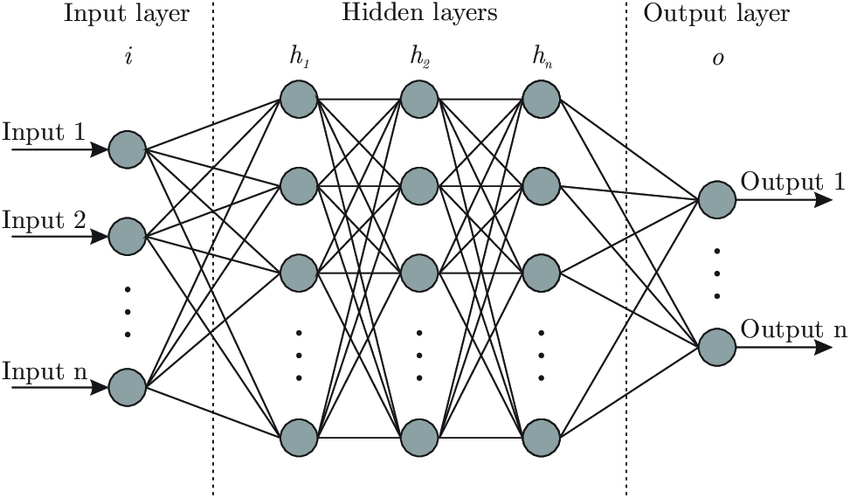
Neurone formel (ou artificiel)

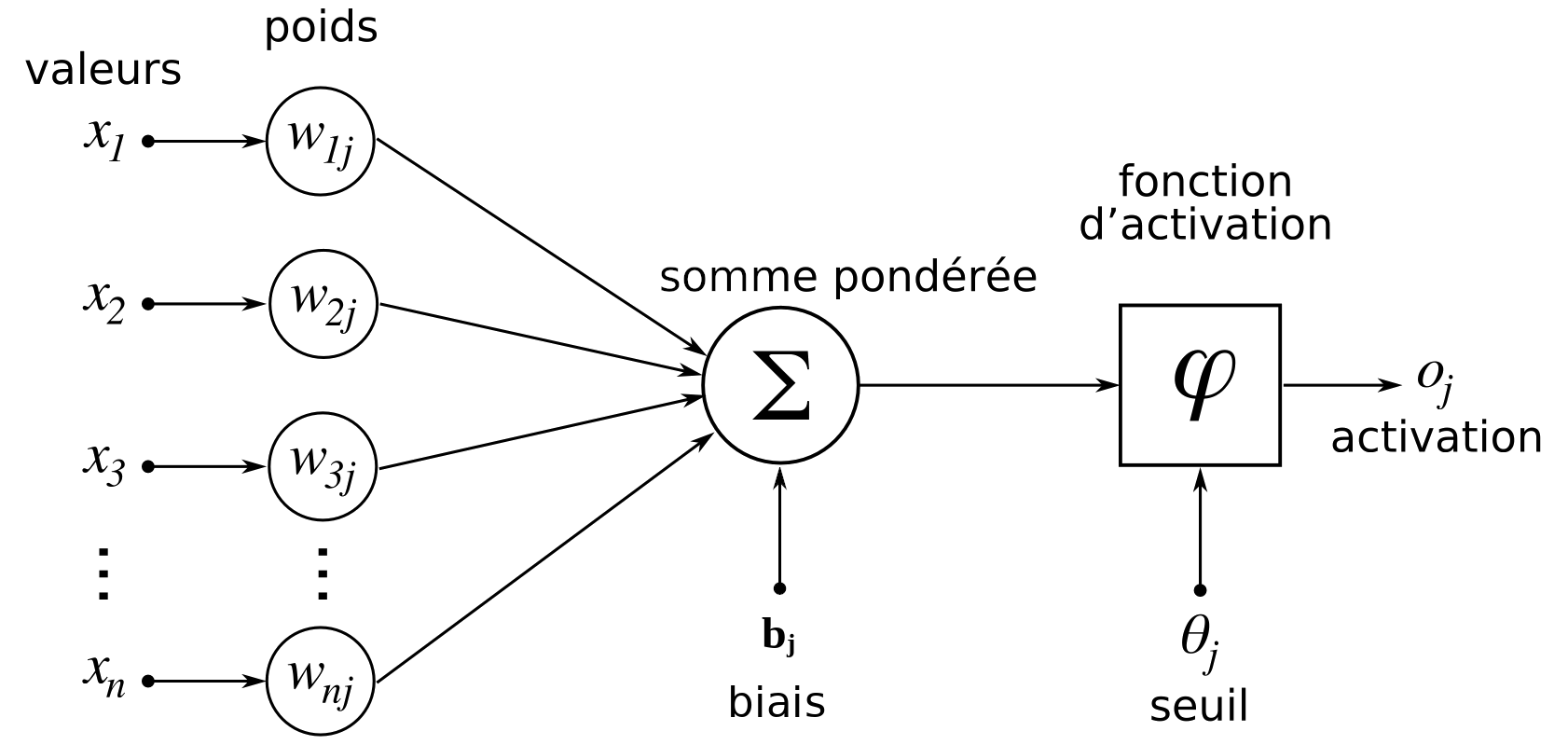
$o_j = \varphi \left( b_j + \sum_{i=1}^{n} w_{ij} x_i \right)$

Fonction d'activation

$\varphi: \mathbb{R} \rightarrow \mathbb{R}$, souvent croissante (voire bornée)

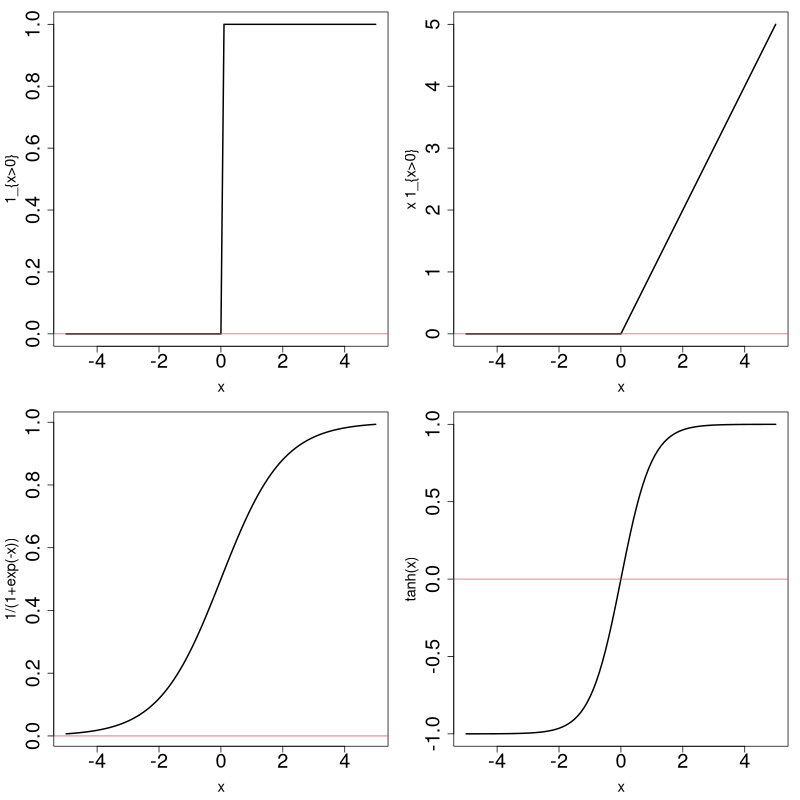
Une fonction adaptée à un type de problème...

Régression

library(neuralnet)
vec_11 = rep(c(-1,1),each=5)
df = data.frame(x=vec_11, y=vec_11)
nn = neuralnet(y ~ ., df,
  linear.output=TRUE,      #pas de transformation en sortie
  act.fct = function(x) x, #activation = identité
  hidden=0)                #...cf suite du cours :-)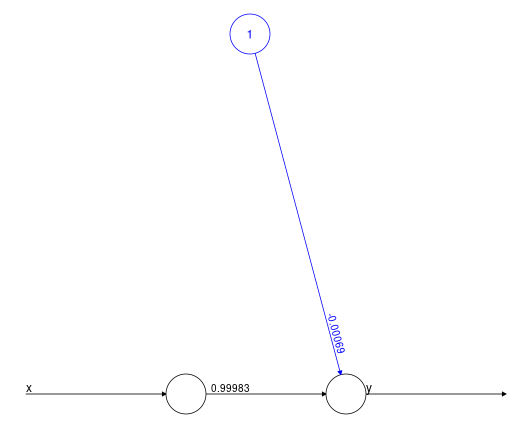

= (très) Simple
régression linéaire

Exemple plus complexe

library(car)
nn = neuralnet(prestige ~ education+income+women, Prestige,
  linear.output=TRUE, act.fct = function(x) x, hidden=0)
plot(nn)

On retrouve les résultats du cours 6 (fonction lm...)

Apprentissage

Illustration sur un exemple simple, lui-même issu du livre "Réseaux neuronaux" de Jean-Philippe Rennard.

Objectif = reconnaître un motif précis sur un carré de 4 pixels noirs ou blancs.

Mise à jour des poids

Itérations (activation = Heaviside)

1. $w_1 = \dots = w_4 = 0, w_0 = 2$ (exemple 1001)
2. $w_1 = 1, w_2 = w_3 = 0, w_4 = 1, w_0 = 1$
   (1001, ok)
3. $w_1 = 0, w_2 = w_3 = -1, w_4 = 0, w_0 = 2$
   (1111, ok)
4. $w_1 = 1, w_2 = w_3 = -1, w_4 = w_0 = 1$
   (1001, ok)
5. etc...

Question : toujours convergence ?

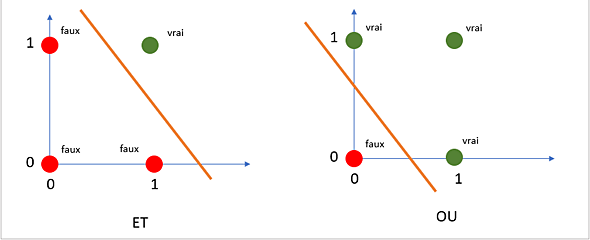
Linéairement séparable ?

Perceptron = (hyper)plan : au-dessus ou en dessous...

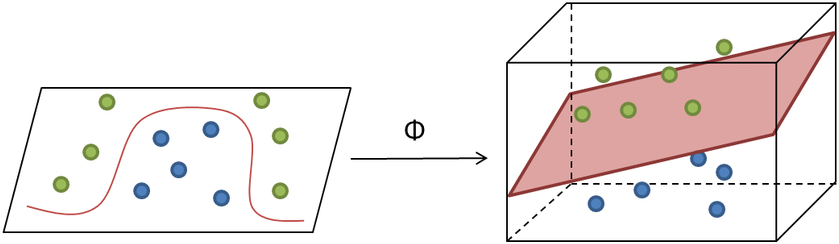
Esquisse code Scala

Couches cachées

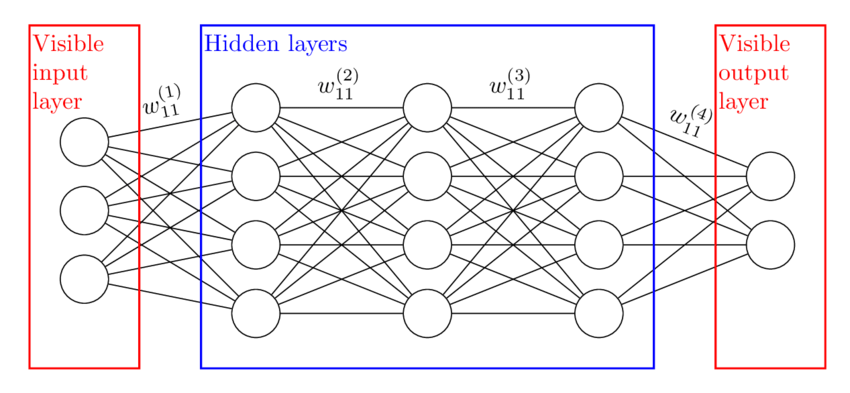
Exemple

softplus <- function(x) log(1 + exp(x))
nn <- neuralnet(
  (Species == "setosa") ~ Petal.Length + Petal.Width,
  iris, linear.output = FALSE,
  hidden = c(3, 2), act.fct = softplus)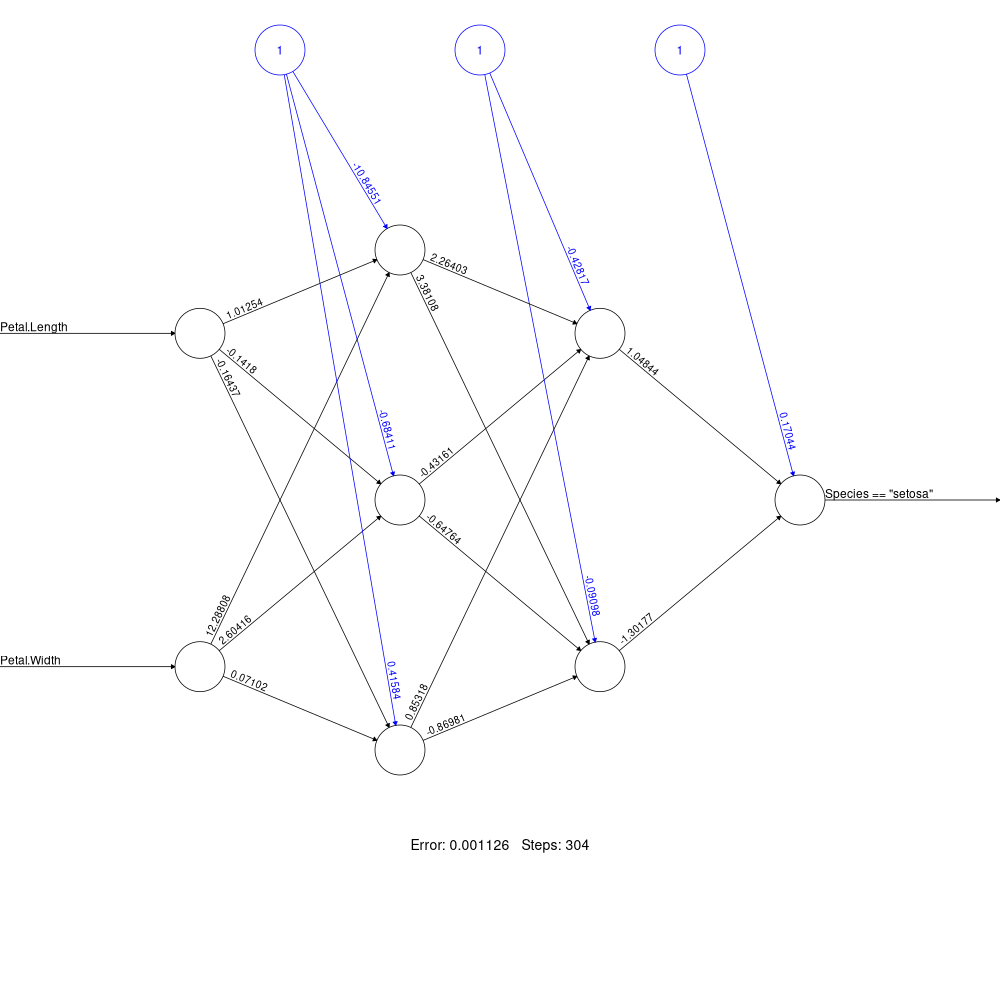

Quelques mots sur l'apprentissage

L'idée est d'évaluer l'impact d'une variation des poids sur l'erreur finale. Pour cela on calcule la dérivée de l'erreur en remontant petit à petit dans le réseau.

Voir la fin de cette présentation, et pour les calculs, la page Wikipedia par exemple.

Illustration : XOR

> X = np.array([[0,0],[0,1],[1,0],[1,1]])
> y = np.array([0, 1, 1, 0])

> nn = neural_network.MLPClassifier(
  hidden_layer_sizes=(3,), max_iter=2000)
> clf = nn.fit(X, y)
> clf.predict(X)
array([0, 0, 1, 0])

> nn = neural_network.MLPClassifier(
  hidden_layer_sizes=(6,), max_iter=2000)
> clf = nn.fit(X, y)
> clf.predict(X)
array([0, 1, 1, 0])

# clf.coefs_
# clf.intercepts_

Illustration MNIST

Source.

Comparaison avec PPR

PPR : une seule couche cachée, addition en sortie (pas de transformation). Fonctions d'activations adaptées aux données.

MLP : $n$ couches cachées, transformation en sortie. Fonctions d'activations fixées.

$\rightarrow$ Ce dernier point permet plus de parallélisme dans l'apprentissage des MLP versus PPR (? à vérifier...)

Exercice

Lisez cet article puis implémentez la méthode.

Variantes

• RPSLS (+ Lizard + Spock).
• Considérer un match nul comme une défaite.

Essayez aussi de faire jouer cet algorithme contre ceux du TP "Chaînes de Markov".

Pour approfondir un peu

Voir aussi l'aide scikit-learn et l'aide tensorflow.