Idée générale
Approximer une sortie $y$ par une combinaison linéaire des variables d'entrée $x_1, \dots, x_m$.
Exemple avec $m = 3$ :
$y = 2 x_1 - x_2 + 1.5 x_3$
Avec peut-être,
- $y$ = vitesse du vent aujourd'hui
- $x_1$ = vitesse du vent hier
- $x_2$ = vitesse du vent avant-hier
- $x_3$ = écart de pression hier/aujourd'hui
Régression affine simple (dimension 1)
$y = a_0 + a x$
> library(car)
> m = lm(prestige ~ education, data=Prestige)
> m$coefficients
(Intercept) education
-10.731982 5.360878
> Prestige[sample(1:nrow(Prestige), 5), c(1, 4)]
education prestige
plumbers 8.33 42.9
sales.clerks 10.05 26.5
office.clerks 11.00 35.6
psychologists 14.36 74.9
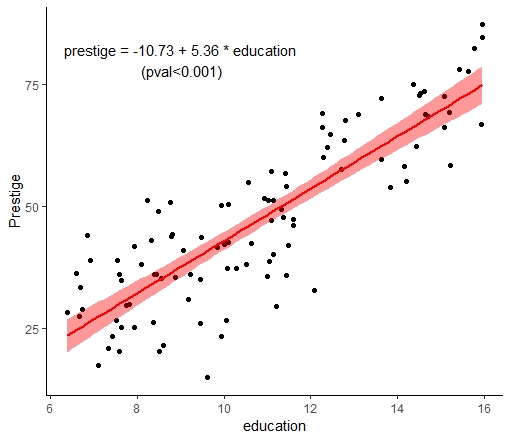
civil.engineers 14.52 73.1prestige $\simeq 5$ education $- 10$
Visualisation
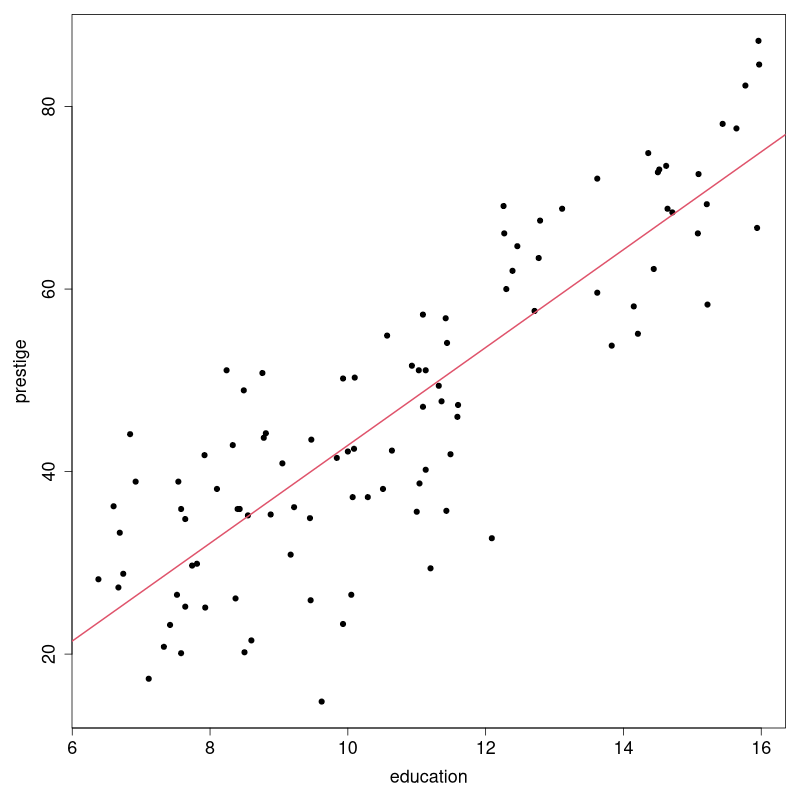
Qualité du modèle :
"(Adjusted) R-squared"
$\simeq 1 -$ erreur relative
> summary(m)
(...)
Multiple R-squared: 0.7228,
Adjusted R-squared: 0.72
# Calcul manuel :
> r <- m$residuals
> f <- m$fitted.values
> mss <- sum((f - mean(f))^2)
> rss <- sum(r^2)
> r2 <- mss / (mss + rss)Régression affine multiple
$y = a_0 + a_1 x_1 + a_2 x_2 + \dots + a_m x_m$
> library(car)
> m = lm(prestige ~ education+income+women, data=Prestige)
> m$coefficients
(Intercept) education income women
-6.794334203 4.186637275 0.001313560 -0.008905157> Prestige[indices,1:4]
education income women prestige
mining.engineers 14.64 11023 0.94 68.8
psychologists 14.36 7405 48.28 74.9
nurses 12.46 4614 96.12 64.7
sales.supervisors 9.84 7482 17.04 41.5
# ...On comprend mieux ! (Année 1971)Qualité $\simeq 0.79$ : peu d'amélioration.
Visualisation / plot(Prestige[,1:4)]

Problème potentiel
> d = data.frame(
x1 = c(1.01, 1),
x2 = c(1, 1.01),
y = c(0, 1))
> d
x1 x2 y
1.01 1.00 0
1.00 1.01 1
# Régression affine
> lm(y ~ ., d)
Coefficients:
(Intercept) x1 x2
101 -100 NA
# Régression linéaire
> lm(y ~ . - 1, d)
Coefficients:
x1 x2
-49.75 50.25Pénalisation
Idée = forcer les coefficients à ne pas prendre de grandes valeurs. Minimiser...
- erreur + $\lambda \sum_{i=1}^{m} |a_i|^2$ = régression ridge.
- erreur + $\lambda \sum_{i=1}^{m} |a_i|$ = régression LASSO.
> library(glmnet)
# Ridge:
> g = glmnet(d[,1:2], d[,3], alpha=0, lambda=10)
> c(g$a0, as.numeric(g$beta))
0.500000 -4.545455 4.545455
# LASSO:
> g = glmnet(d[,1:2], d[,3], alpha=1, lambda=1)
> c(g$a0, as.numeric(g$beta))
0.5 0.0 0.0Ridge & LASSO en images
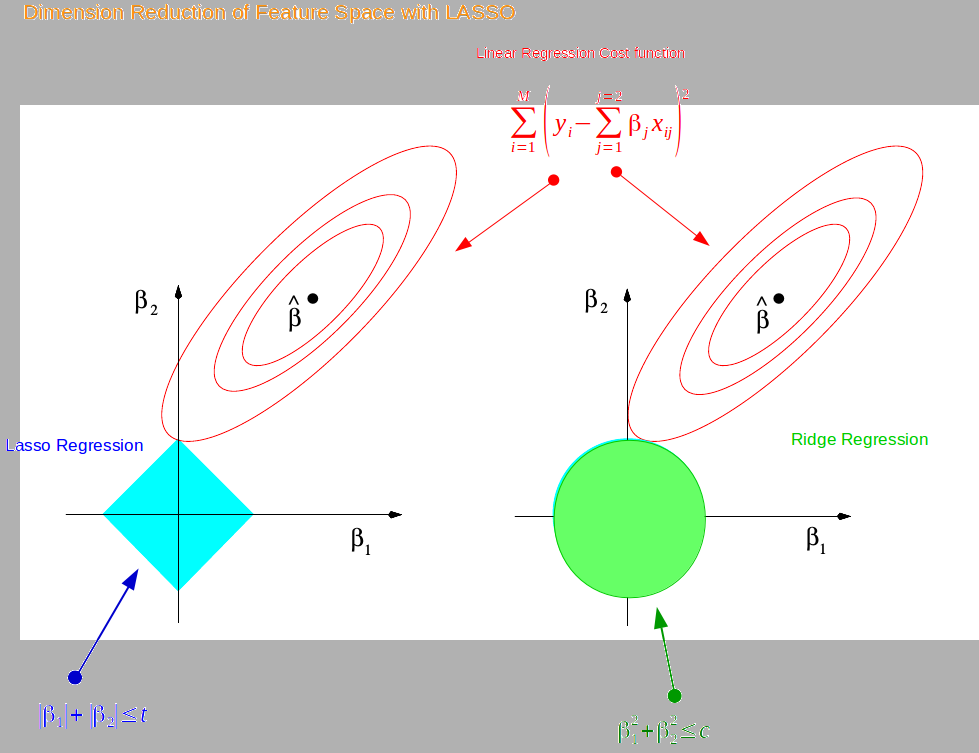
[Hors "programme" :] Présentation Ridge + LASSO
Prédiction
> library(glmnet)
> d = read.csv("https://archive.ics.uci.edu/ml/machine-learning-databases/communities/communities.data", header=F, na.strings="?")
> d = d[,-4]
> indices = which(apply(d, 1, function(r) all(!is.na(r))))
> d = d[indices,]
> dim(d)
123 127 #plus de colonnes que de lignes> m0 = lm(V128 ~ ., d)
# Des warnings, fit parfait : normal
> x = as.matrix(d[,-127])
> y = as.matrix(d[,127])
> m1 = cv.glmnet(x, y, alpha=1) #LASSO
> p1 = predict(m1, x, s=m1$lambda.min)
> rss = sum( (p1 - y)^2 )
> mss = sum( (p1 - mean(p1))^2 )
> mss / (rss + mss)
0.87 #pas mal, et...sum(m1$glmnet.fit$beta[,m1$index[1]] != 0.0)
# Seulement 27 coefficients non nuls !Recette
Si relativement peu de variables :
régression linéaire (multiple).
Si warnings, considérer régression ridge.
Si (relativement) beaucoup de variables :
régression LASSO.
Généralisations
Idée 1 : fabriquer une nouvelle variable.
> library(glmnet)
# "Indice d'obésité" en fonction de taille/poids
> d = read.csv("https://raw.githubusercontent.com/chriswmann/datasets/master/500_Person_Gender_Height_Weight_Index.csv")
> m0 = lm(Index ~ Height+Weight, d)
R2 = 0.83 #pas mal, mais...# Ajout logique de l'IMC
> d['BMI'] = d['Weight'] / (d['Height']/100)^2
> m0 = lm(Index ~ Height+Weight+BMI, d)
R2 = 0.87 #un peu mieuxIdée 1 bis : régression polynomiale.
$$y = a_0 + a_1 x + a_2 x^2 + \dots + a_d x^d$$
Idée 2 : fonctions non linéaires = GAM
$$y = a_0 + f_1(x_1) + f_2(x_2) + \dots + f_m(x_m)$$
Idée 3 : généralisation de GAM = PPR
$$y = a_0 + f_1(\beta_1 x) + f_2(\beta_2 x) + \dots + f_d(\beta_d x)$$
Utilisation en R
> library(mgcv)
> gam(Petal.Length ~ s(Sepal.Width) +
s(Sepal.Length) +
s(Petal.Width),
data=iris)
> ppr(Petal.Length ~ ., iris, nterms=5)Essayer les fonctions summary(), plot() ...
Complément : optimisation PPR
$$\arg\min_{\beta, f} \sum_{i=1}^{n} \left[ y_i - \sum_{j=1}^{r} f_j(\beta_j x_i) \right]^2$$ $\rightarrow$ Impossible, donc on optimise "pas à pas" :
- Trouver $\beta_1, f_1$ minimisant $\sum_{i=1}^{n} [y_i - f_1(\beta_1 x_i)]^2$
- Noter $r_i = y_i - f_1(\beta_1 x_i)$ les résidus, et
trouver $\beta_2, f_2$ minimisant $\sum_{i=1}^{n} [r_i - f_2(\beta_2 x_i)]^2$ - ...etc (jusqu'à avoir $r$ termes).
Exercice 1
Cherchez à prédire le nombre de personnes au chômage (variable 'unemploy') en fonction des autres, avec le jeu de données economics.
Vous pouvez éventuellement vous inspirer de / comparer avec cette page.
Exercice 2
Cherchez à prédire...
- la variable 'Volume' du dataset 'trees'
- la variable 'Employed' du dataset 'longley'
Les deux sont dans le package 'datasets' :
library(datasets)
data(trees)
data(longley)