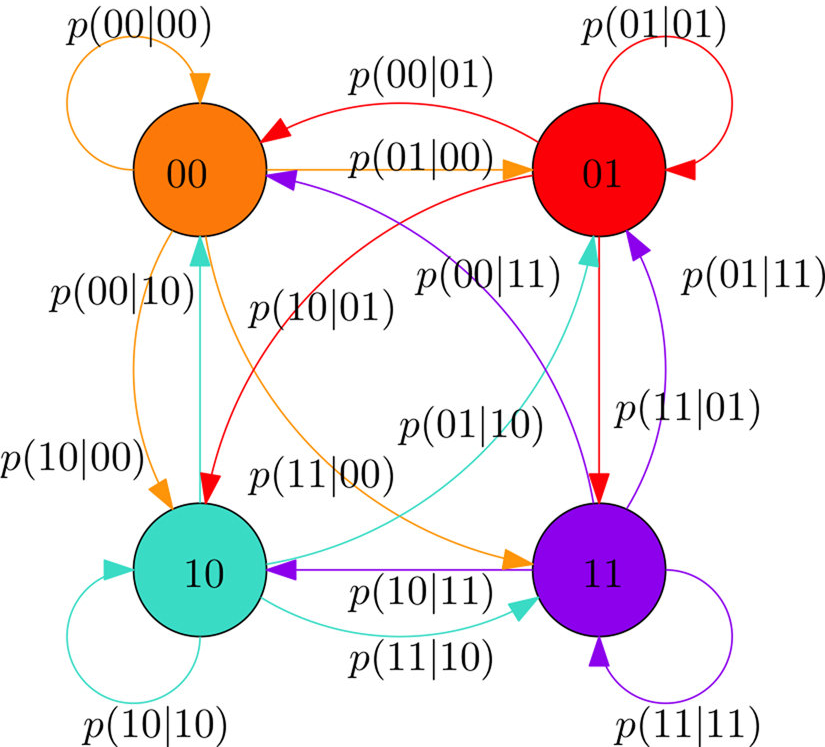
Motivations
Décrire l'évolution d'un système où l'état courant détermine les probabilités de se trouver dans un autre état après changement.
Exemples :
- Roulette au casino
- Niveau dans un jeu vidéo
- Marche aléatoire dans un labyrinthe
-
Niveau de pollution -
Recette de cuisine
Introduction
Chaîne de Markov = états + transitions.
Exemple : état = progression dans un jeu
États = jouer au niveau 1, 2, contre le boss final (B)
avoir perdu (P)
avoir terminé le jeu (T)
- Transitions $1 \rightarrow 2, P$ ; $2 \rightarrow B, P$ ; $B \rightarrow P, T$
- États $P$ et $T$ terminaux (on y reste !)
Probabilités de transition ?
Matrice $P \Leftrightarrow$ graphe de transition
$$\begin{pmatrix} 0.0 & 0.7 & 0.0 & 0.3 & 0.0\\ 0.0 & 0.0 & 0.5 & 0.5 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.8 & 0.2\\ 0.0 & 0.0 & 0.0 & 1.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{pmatrix}$$
import pydtmc as m
P = [
[0.0, 0.7, 0.0, 0.3, 0.0],
[0.0, 0.0, 0.5, 0.5, 0.0],
[0.0, 0.0, 0.0, 0.8, 0.2],
[0.0, 0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0]]
mc = m.MarkovChain(P,
['1', '2', 'B', 'P', 'T'])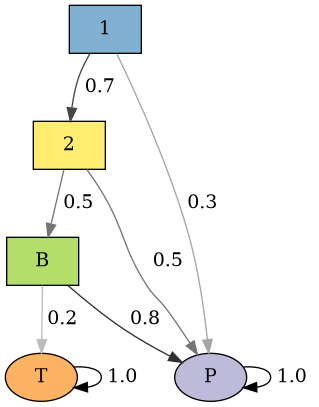
Découpage de $P$
$$\left[ \begin{array}{ccc|cc} \color{red}{0.0} & \color{red}{0.7} & \color{red}{0.0} & 0.3 & 0.0 \\ \color{red}{0.0} & \color{red}{0.0} & \color{red}{0.5} & 0.5 & 0.0 \\ \color{red}{0.0} & \color{red}{0.0} & \color{red}{0.0} & 0.8 & 0.2 \\ \hline 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{array} \right]$$
États "transients" en haut à gauche: matrice $Q$.
États "absorbants" en bas à droite.
Matrice fondamentale
$$N = (I - Q)^{-1}$$
$N[i,j]$ = nombre de passages moyen par l'état $j$
si on commence en $i$
Sur l'exemple, [code: mc.fundamental_matrix]
$$N = \begin{pmatrix} 1 & 0.7 & 0.35 \\ 0 & 1.0 & 0.50 \\ 0 & 0.0 & 1.00 \end{pmatrix}$$
Calculs / en vert = matrice $R$.
$$\left[ \begin{array}{ccc|cc} 0.0 & 0.7 & 0.0 & \color{green}{0.3} & \color{green}{0.0} \\ 0.0 & 0.0 & 0.5 & \color{green}{0.5} & \color{green}{0.0} \\ 0.0 & 0.0 & 0.0 & \color{green}{0.8} & \color{green}{0.2} \\ \hline 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{array} \right]$$
Temps moyen avant état absorbant depuis $i$ =
somme des éléments de la $i^{eme}$ ligne de $N$.
Probabilité d'être absorbé en $j$ depuis $i$ =
coefficient $(i,j)$ de $B = N R$.
Avec PyDTMC
> mc.absorption_times
array([2.05, 1.5 , 1. ])Environ 2 "temps" avant un état absorbant depuis le niveau 1. "1.5" depuis le niveau 2, et 1 depuis le 3.
> mc.absorption_probabilities
array([[0.93, 0.9 , 0.8 ],
[0.07, 0.1 , 0.2 ]])Probabilité autour de 0.9 de perdre si on commence au niveau 1 ou 2. 0.8 / 0.2 logique (pourquoi ?)
Chaînes non absorbantes
Exemple : état = niveau à Tetris (vitesse...)
Deux possibilités :
- passer au niveau suivant (s'il y en a un).
- revenir au niveau 1 (si on perd).
Supposons 4 états (= 4 niveaux).
Chemin possible : 1, 2, 3, 4, 1, 2, 1
Probabilités de transition ?
Matrice $P \Leftrightarrow$ graphe de transition
$$\begin{pmatrix} 0.3 & 0.7 & 0.0 & 0.0\\ 0.4 & 0.0 & 0.6 & 0.0\\ 0.6 & 0.0 & 0.0 & 0.4\\ 0.8 & 0.0 & 0.0 & 0.2 \end{pmatrix}$$
import pydtmc as m
P = [
[0.3, 0.7, 0.0, 0.0],
[0.4, 0.0, 0.6, 0.0],
[0.6, 0.0, 0.0, 0.4],
[0.8, 0.0, 0.0, 0.2]]
mc = m.MarkovChain(P,
['1','2','3','4'])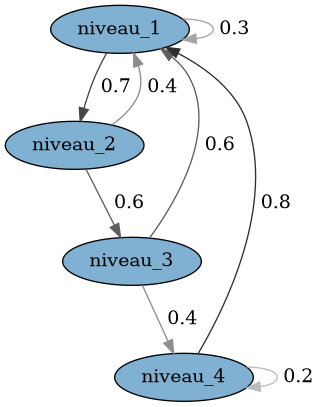
Définitions, propriétés
$P^n$ = matrice des transitions en $n$ étapes.
$P$ est régulière si $\exists n / P^n > 0$
# Test :
> mc.is_ergodic
TrueSi $P$ est régulière, $\exists ! w / w P = w$
$w$ = distribution stationnaire.
$\propto$ temps moyen passé dans chaque état.
> mc.stationary_distributions
[array([0.42918455, 0.30042918, 0.18025751, 0.09012876])]Temps d'atteinte ($P$ régulière...)
Temps moyen depuis $i$ avant de revenir en $i$ ( = $r_i$) ?
> mc.recurrence_times
array([ 2.33, 3.32857143, 5.54761905, 11.0952381 ])$r_i = 1 / w_i$
Temps moyen pour arriver à $j$ en partant de $i$ ?
> mc.mean_first_passage_times_between(['1'], ['4'])
12.619047619047619Astuce = considérer 4 comme absorbant.
$\rightarrow$ Retour au cas précédent.
Promenade
m.plot_walk(mc, 20, '1', plot_type='sequence')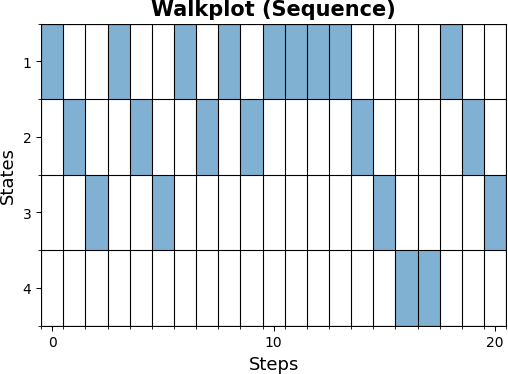
Approche prédictive I
On vous donne une (longue) suite d'états.
Déterminer une chaîne y correspondant.
mc_est = mc.fit_walk(
'map',
['1','2','3','4'],
mc.walk(100, '1'))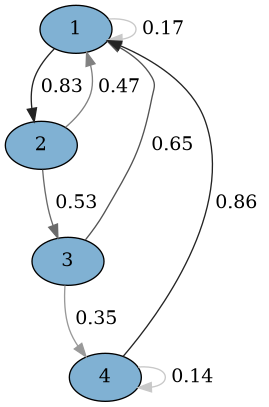
Approche prédictive II
On vous donne une suite d'états.
A-t-elle été générée par la chaîne $mc$ ?
> mc.walk_probability(
['1','2','3','1','2','3','1','2','1','2'])
0.012446783999999994
> mc.walk_probability(
['1','1','1','2','3','4','4','4','4','4'])
2.4191999999999995e-05Application : détection d'anomalies.
Exercice 1
Le chat "markovien" Gribouille ne réalise que 3 actions dans sa journée : dormir, manger et jouer.
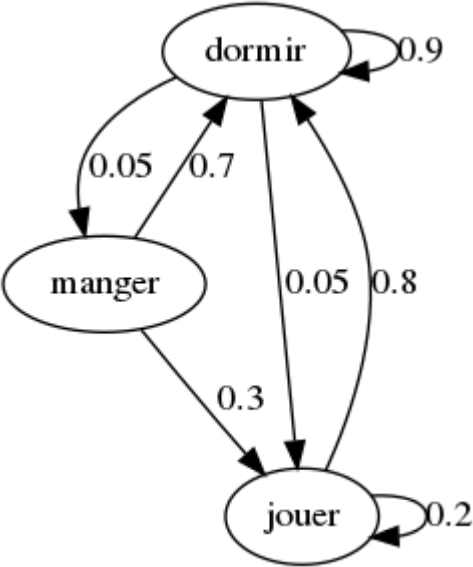
- À $t=5$, Gribouille dort. À $t=8$, quelle est la probabilité qu'il joue ?
- À $t=0$, Gribouille mange. À $t=12$, quelle est la probabilité qu'il dorme ?
- Calculez la distribution stationnaire.
- À $t=10$, Gribouille dort. Au bout de combien de temps en moyenne mangera-t-il ?
Exercice 2
Pour sortir de prison sous caution, Albert doit
payer 8€. Il n'a que 3€ sur lui.
Un gardien lui propose un jeu (en plusieurs tours) :
- Si Albert parie A€, il gagne A€ avec probabilité 0.4
- Sinon, il perd A€ avec probabilité 0.6
Probabilité qu'Albert sorte de prison ainsi ?
Stratégie optimale ?
Suggestion de corrigé
Note "hors programme"
Je n'ai pas parlé de...
- chaînes de Markov à temps discret mais espace d'état infini,
- chaînes de Markov à temps continu,
- chaînes dont la matrice de transition dépend du temps.
Ces trois situations sont évidemment intéressantes mais nécessitent + de rappels mathématiques. Voir par exemple Probabilités et processus stochastiques (Yves Caumel 2011).