
Motivations
- Détection de communautés (réseaux sociaux...)
- Classification d'interactions protéine-protéine
- Analyse d'un réseau informatique, etc
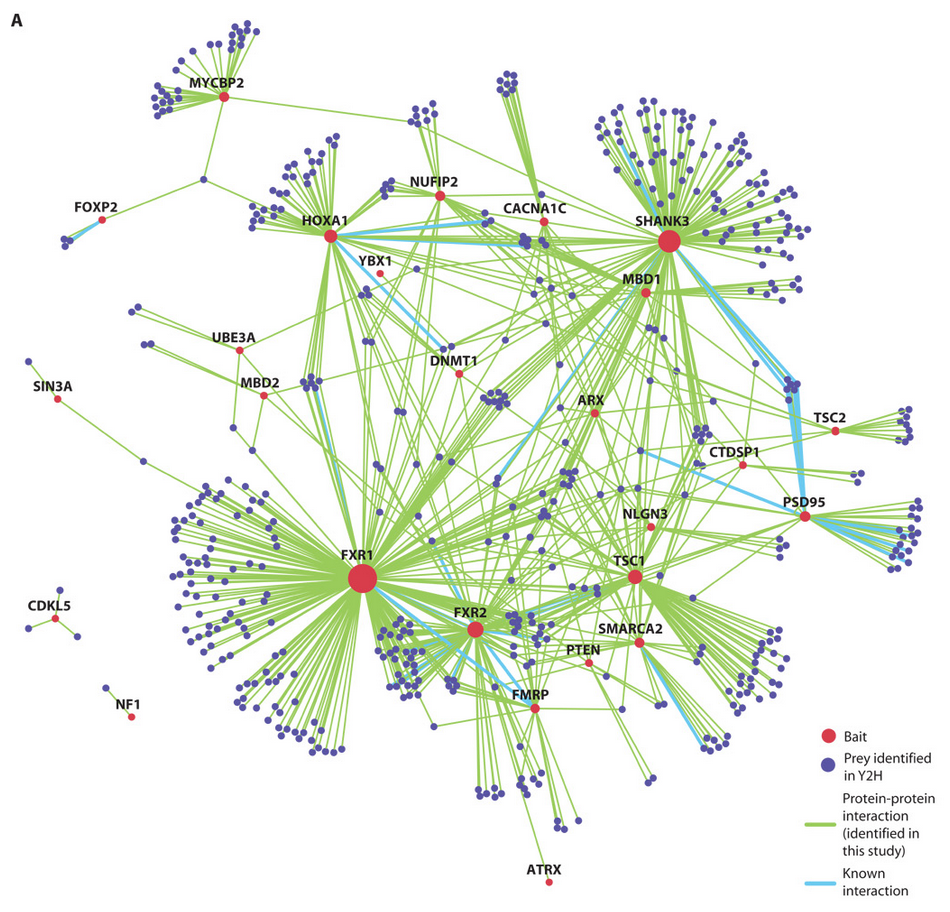
Des données au graphe

Construction d'un graphe ?
Cas facile : les données sont déjà dans un graphe (réseaux sociaux).
Cas moins simple : les données sont dans ${\cal R}^n$
- Relier les points à distance $< \varepsilon$ ($\varepsilon$ = ?)
- Relier les points à leurs $k$ plus proches voisins
Avec R :
library(nngd)
g = nng(data, k=1, mutual=FALSE)1-PPV
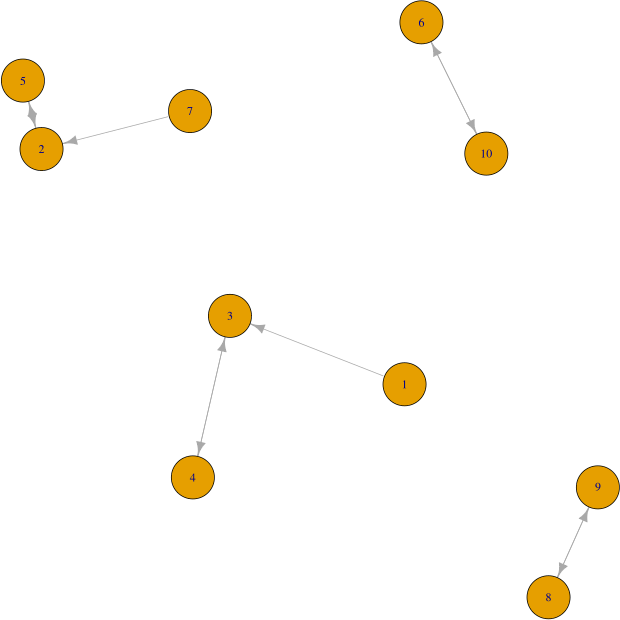
g = nng(data, k=3, mutual=TRUE)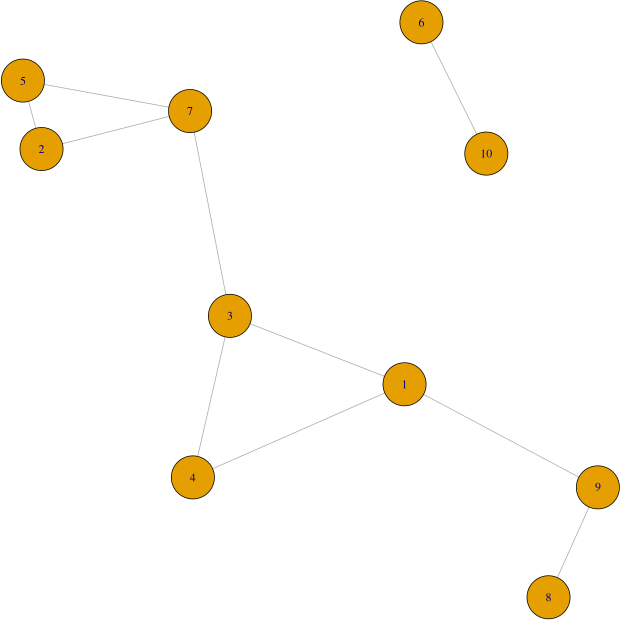
g = nng(data, k=4, mutual=TRUE)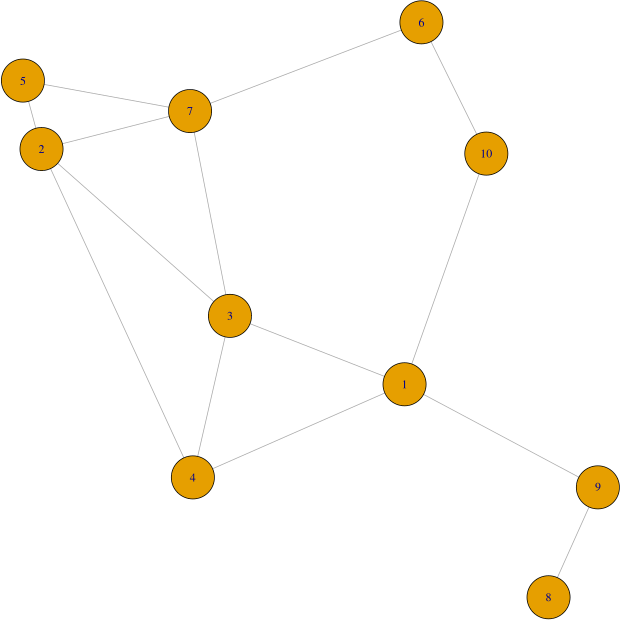
Idée naturelle : poids d'une arête = distance (euclidienne) inter-points. Puis, (nouvelle) distance = longueur du plus court chemin.
d1 = as.matrix(dist(data))
E = as_edgelist(g, names=F)
weights = apply(E, 1, function(r) d1[r[1],r[2]])
d2 = distances(g, weight=weights)
> d1[5,8]
[1] 4.19793
> d2[5,8]
[1] 4.857773Quelques différences (même) sur cet exemple simple.
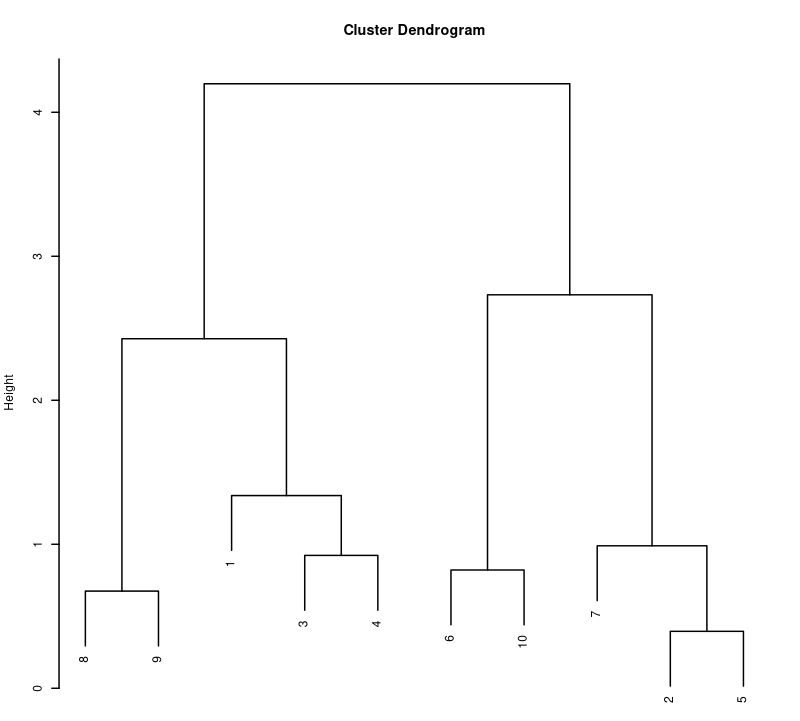

avec la distance "plus court chemin".
Un autre point de vue...
Idée : déduire une partition directement de la structure du graphe (des plus proches voisins).
Un sous-ensemble de sommets tous connectés n'a a priori pas de raison d'être séparé.
Exemple Facebook : $A \leftrightarrow$ (ami avec) $B \leftrightarrow C \leftrightarrow D$.
Sans plus d'informations, on les regroupe ?
Et si en plus, $D \leftrightarrow A \leftrightarrow C$ et $B \leftrightarrow D$ ?
Algorithme "voisins communs"
Poids d'une arête = nombre de sommets dans l'intersection des voisinages.
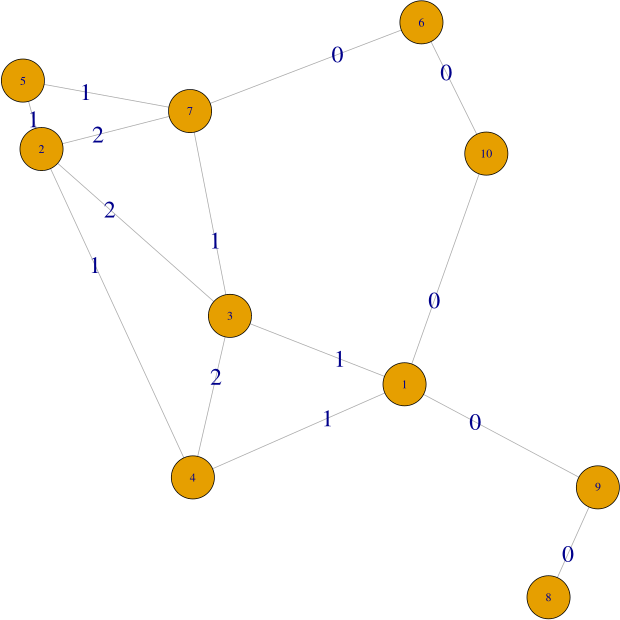
Seuil 2 :
4,3,2,7 regroupés.
Seuil 1 :
1,2,3,4,5,7 regroupés.
Arbre couvrant de poids minimal (ACM)
On suppose le graphe connexe.
Arbre couvrant = sous-graphe sans cycle
contenant tous les sommets.
De poids minimal si la somme des poids
des arêtes de l'arbre est minimale.
Idée : supprimer les $K-1$ arêtes de l'ACM
de plus grand poids $\Rightarrow K$ clusters.
# MST : Minimum Spanning Tree
plot( mst(g, weights=weights) )
Note : doc intéressante.
Clustering spectral
TODO:
- Définition du problème
- Laplacien du graphe
- Optimum approché via $L$
Temps moyen d'aller-retour
On part du sommet $i$ puis on passe sur un sommet voisin choisi au hasard, et on recommence, etc, jusqu'à arriver en $j$ ...Puis on revient en $i$.
Distance$(i, j)$ = poids du chemin parcouru.
Problème : comment "choisir un voisin au hasard" ?
- Définition d'une similarité $s(i,j) \geq 0$
- Probabilité de saut $i \rightarrow j \propto s(i, j)$
Distance $\rightarrow$ Similarité
Similarité augmente si distance diminue.
- Idée 0 : $s(i,j) = 1$ (sans distances)
- Idée 1 : $s(i,j) = d_{max} - d(i,j)$
- Idée 2 : $s(i,j) = e^{-d(i,j) / \sigma}$
Ensuite, $$\mathbb{P}(i,j) = \frac{s(i,j)}{\sum_{k=1}^{v_i} s(i,k)} \, ,$$ avec $1, \dots, v_i$ voisins de $i$.
Avec R : commute-time distances
library(nngd); o <- nng(data)
distances <- ectd(o) #matrice n x n
# Puis p <- pam(distances, ...), ou :
h <- hclust(as.dist(distances), method="ward.D")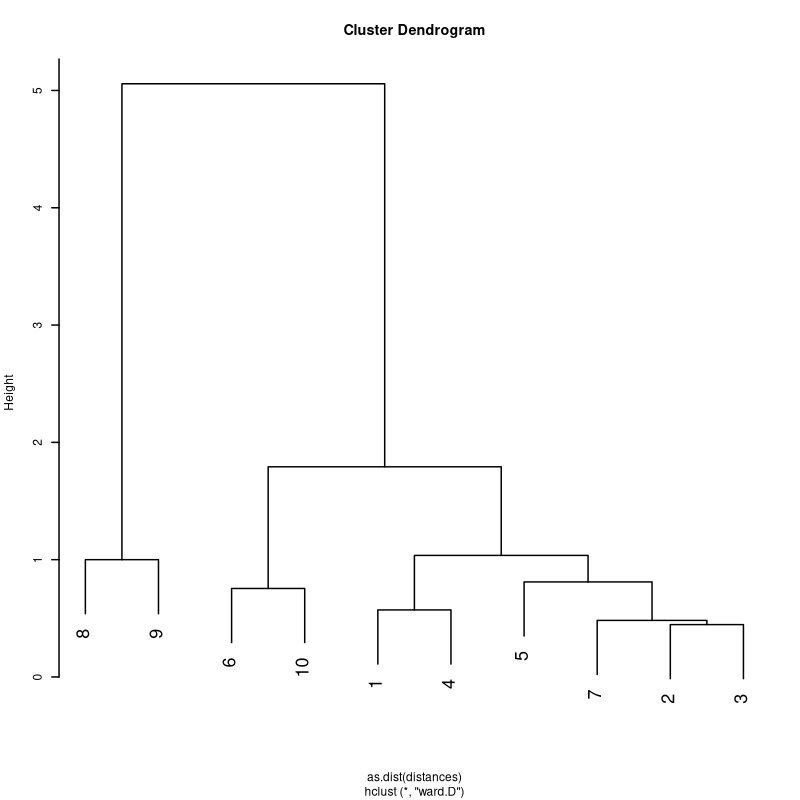
Sur données iris (k=40)
o <- nng(iris[,-5], k=40)
dists = ectd(o, similarity=function(x) exp(-x))
h <- hclust(as.dist(dists)) ; plot(h)
factoextra::fviz_cluster(list(data=iris[,-5], cluster=cutree(h,3)))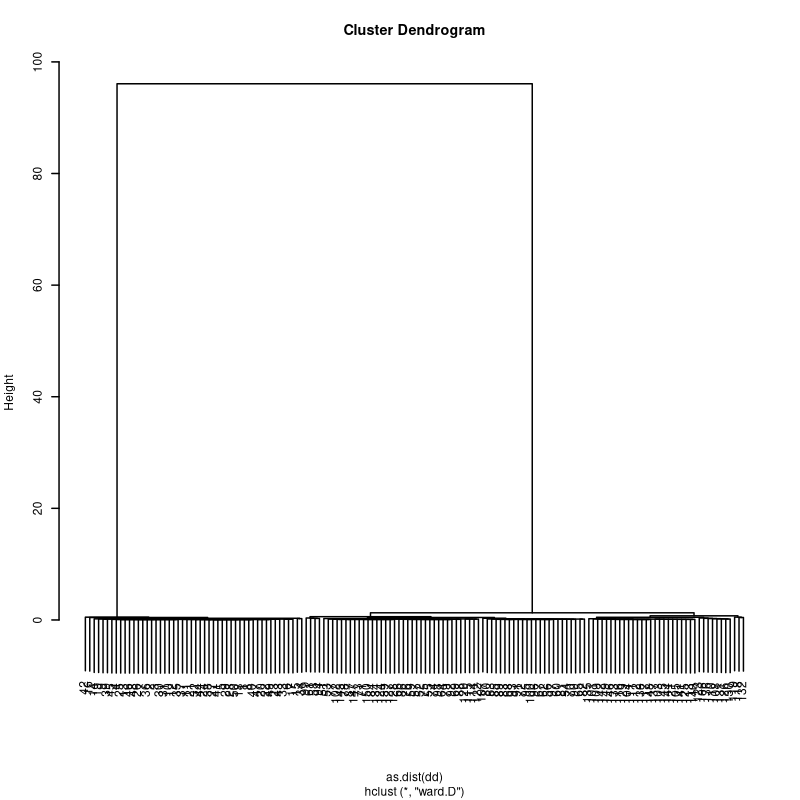

Indique clairement qu'il n'y a que 2 clusters
Choix de $k$ ?
Triche si partition connue :
for (k in 10:50) {
o <- nng(iris[,-5], k=k)
dists = ectd(o, similarity=function(x) exp(-x))
print(paste(k, ":", extCriteria(rep(1:3, each=50),
cutree(hclust(as.dist(dists)), 3),
"Jaccard"))$jaccard)
}Sinon : diverses heuristiques + ou - bonnes...
...Idée/possibilité : $k$ dépendant du point ?
Exercice 1
Reprenez les jeux de données artificiels sur cette page.
Essayez d'obtenir la classification souhaitée en jouant sur les paramètres des algorithmes.
Exercice 2
Testez les algorithmes sur les jeux de données
"karaté" et "dauphins" depuis cette page.
Vous aurez besoin de la fonction igraph::read.graph.
Suggestion de "corrigé"
Note finale
Je n'ai pas parlé d'algorithmes de détection de communautés. igraph en code un certain nombre : fonctions cluster_* en R et community_* en Python.
Voir par exemple ce lien.